Fiona Skerman

Modularity introduced by Newman and Girvan (link) is a popular metric in community detection.

However, little research has been performed to develop efficient modularity calculation algorithms for probabilistic networks. Particularly, it is challenging to efficiently calculate expected modularity when all possible worlds are considered.

To address this problem, we propose two algorithms partitioning the possible worlds based on their modularities to significantly reduce the number of probability calculations. We evaluate the accuracy and time efficiency of our algorithms through comprehensive experiments.

Modularity introduced by Newman and Girvan (link) is a popular metric in community detection.

It is known that complete graphs and complete multipartite graphs have modularity zero. We show that the least number of edges we may delete from the complete graph $K_n$ to obtain a graph with non-zero modularity is $\lfloor n/2\rfloor +1$. Similarly we determine the least number of edges we may delete from or add to a complete bipartite graph to reach non-zero modularity. We give some corresponding results for complete multipartite graphs, and a short proof that complete multipartite graphs have modularity zero.

We also analyse the modularity of very dense random graphs, and in particular we find that there is a transition to modularity zero when the average degree of the complementary graph drops below 1.

Modularity introduced by Newman and Girvan (link) is a popular metric in community detection.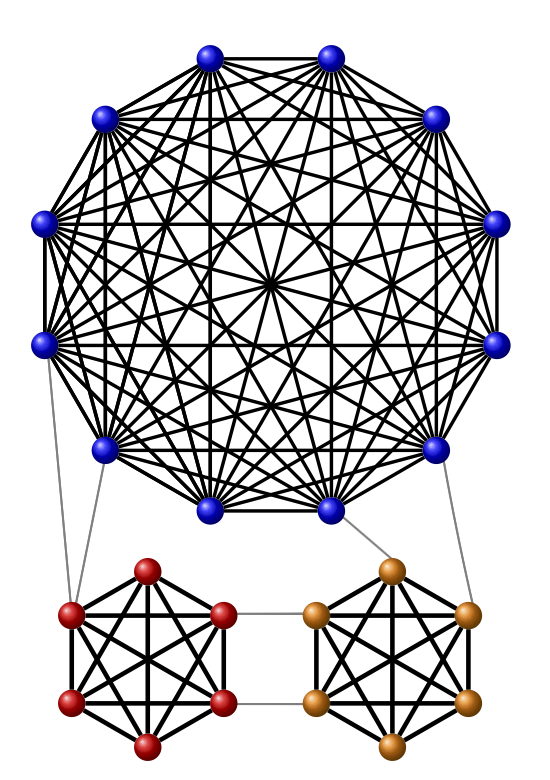

We prove new lower bounds on the modularity of graphs. Specifically, the modularity of a graph $G$ with average degree $\bar d$ is $Ω(\bar{d}^{-1/2})$, under some mild assumptions on the degree sequence of $G$. The lower bound $Ω(\bar{d}^{-1/2})$ applies, for instance, to graphs with a power-law degree sequence or a near-regular degree sequence.

It has been suggested that the relatively high modularity of the Erdős-Rényi random graph $G_{n,p}$ stems from the random fluctuations in its edge distribution, however our results imply high modularity for any graph with a degree sequence matching that typically found in $G_{n,p}$.

The proof of the new lower bound relies on certain weight-balanced bisections with few cross-edges, which build on ideas of Alon (see this paper) and may be of independent interest."

A random permutation $\Pi_n$ of $\{1,\dots,n\}$ follows the $\DeclareMathOperator{\Mallows}{Mallows}\Mallows(n,q)$ distribution with parameter $q>0$ if $\mathbb{P} ( \Pi_n = \pi )$ is proportional to $\DeclareMathOperator{\inv}{inv} q^{\inv(\pi)}$ for all $\pi$. Here $\DeclareMathOperator{\inv}{inv} \inv(\pi) := |\{ i < j : \pi(i) > \pi(j) \}|$ denotes the number of inversions of $\pi$. We consider properties of permutations that can be expressed by the sentences of two different logical languages. Namely, the theory of one bijection ($\mathsf{TOOB}$), which describes permutations via a single binary relation, and the theory of two orders ($\mathsf{TOTO}$), where we describe permutations by two total orders. We say that the convergence law holds with respect to one of these languages if, for every sentence $\phi$ in the language, the probability $\mathbb{P} (\Pi_n\text{ satisfies } \phi)$ converges to a limit as $n\to\infty$. If moreover that limit is in the set $\{0,1\}$ for all sentences, then the zero-one law holds.

We will show that with respect to $\mathsf{TOOB}$ the $\Mallows(n,q)$ distribution satisfies the convergence law but not the zero-one law when $q=1$, when $0 < q < 1$ is fixed the zero-one law holds, and for fixed $q>1$ the convergence law fails.

We will prove that with respect to $\mathsf{TOTO}$ the $\Mallows(n,q)$ distribution satisfies the convergence law but not the zero-one law for any fixed $q\neq 1$, and that if $q=q(n)$ satisfies $1- 1/\log^*n < q < 1 + 1/\log^*n$ then $\Mallows(n,q)$ fails the convergence law. Here $\log^*$ denotes the discrete inverse of the tower function.

Suppose that there is an unknown underlying graph $G$ on a large vertex set, and we can test only a proportion of the possible edges to check whether they are present in $G$. If $G$ has high modularity, is the observed graph $G'$ likely to have high modularity? We see that this is indeed the case under a mild condition, in a natural model where we test edges at random. We find that $q^*(G') \geq q^*(G)-\varepsilon$ with probability at least $1-\varepsilon$, as long as the expected number edges in $G'$ is large enough. Similarly, $q^*(G') \leq q^*(G)+\varepsilon$ with probability at least $1-\varepsilon$, under the stronger condition that the expected average degree in $G'$ is large enough. Further, under this stronger condition, finding a good partition for $G'$ helps us to find a good partition for $G$. Modularity introduced by Newman and Girvan (in this paper) is a popular metric in community detection.

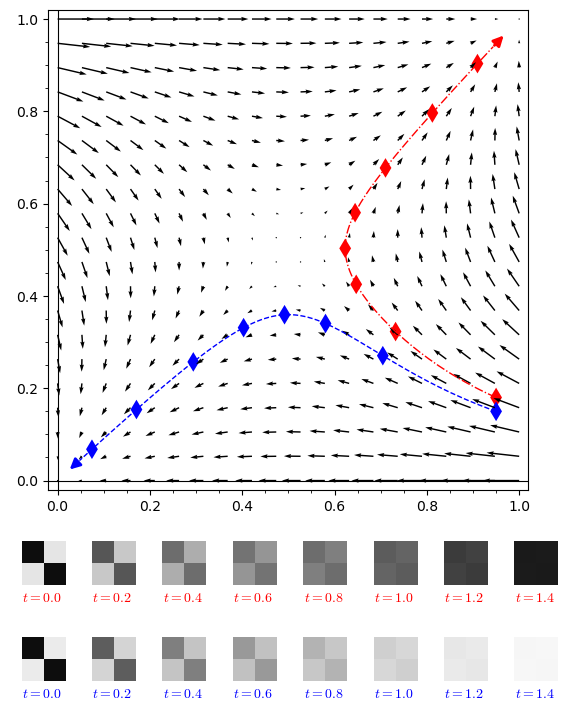We introduce a class of random graph processes, which we call flip processes. Each such process is given by a rule which is a function $\mathscr{R}:\mathscr{H}_k \rightarrow \mathscr{H}_k$ from all labelled $k$-vertex graphs into itself ($k$ is fixed). The process starts with a given $n$-vertex graph $G_0$. In each step, the graph $G_i$ is obtained by sampling $k$ random vertices $v_1,\ldots,v_k$ of $G_{i-1}$ and replacing the induced graph $F:=G_{i-1}[v_1,\ldots,v_k]$ by $\mathscr{R}(F)$. This class contains several previously studied processes including the Erd\H{o}s--R\'enyi random graph process and the triangle removal process. Actually, our definition of flip processes is more general, in that $\mathscr{R}(F)$ is a probability distribution on $\mathscr{H}_k$, thus allowing randomised replacements.

Given a flip process with a rule $\mathscr{R}$, we construct time-indexed trajectories $\Phi: \mathscr{W}_{0} \times [0,\infty)\rightarrow \mathscr{W}_{0}$ in the space of graphons. We prove that for any $T > 0$ starting with a large finite graph $G_0$ which is close to a graphon $W_0$ in the cut norm, with high probability the flip process will stay in a thin sausage around the trajectory $(\Phi(W_0,t))_{t=0}^T$ (after rescaling).

These graphon trajectories are then studied from the perspective of dynamical systems. Among others topics, we study continuity properties of these trajectories with respect to time and initial graphon, existence and stability of fixed points and speed of convergence (whenever the infinite time limit exists). We give an example of a flip process with a periodic trajectory.

See also the paper Prominent examples of flip processes.

We define a graph process $G(p,q)$ based on a discrete branching process with deletions and mergers, which is inspired by the 4-cycle structure of both the hypercube $Q_d$ and the lattice $\mathbb{Z}^d$ for large $d$. Individuals have Poisson offspring distribution with mean $1+p$ and certain deletions and mergers occur with probability $q$; these parameters correspond to the mean number of edges discovered from a given vertex in an exploration of a percolation cluster and to the probability that a non-backtracking path of length four closes a cycle, respectively.

We prove survival and extinction under certain conditions on $p$ and $q$ that heuristically match the known expansions of the critical probabilities for bond percolation on the lattice $\mathbb{Z}^d$ and the hypercube $Q_d$. These expansions have been rigorously established by Hara and Slade in 1995, and van der Hofstad and Slade in 2006, respectively. We stress that our method does not constitute a branching process proof for the percolation threshold.

The analysis of the graph process survival is considerably more challenging than for branching processes in discrete time, due to the interdependence between the descendants of different individuals in the same generation. In fact, it is left open whether the survival probability of $G(p,q)$ is monotone in $p$ or $q$; we discuss this and some other open problems regarding the new graph process.

We relate two important notions in graph theory: expanders which are highly connected graphs, and modularity a parameter of a graph that is primarily used in community detection. More precisely, we show that a graph having modularity bounded below 1 is equivalent to it having a large subgraph which is an expander.

We further show that a connected component $H$ will be split in an optimal partition of the host graph $G$ if and only if the relative size of $H$ in $G$ is greater than an expansion constant of $H$. This is a further exploration of the resolution limit known for modularity, and indeed recovers the bound that a connected component $H$ in the host graph $G$ will not be split if $e(H)<\sqrt{2e(G)}$.

A structural and geometric property of graphs is the presence of large expanders. The problem of finding such structures was considered by Krivelevich in this paper. Here, we show that the problem of finding a large induced subgraph that is an expander can be reduced to the simpler problem of finding a topological minor that is an expander. Our proof is constructive, which is helpful in an algorithmic setting.
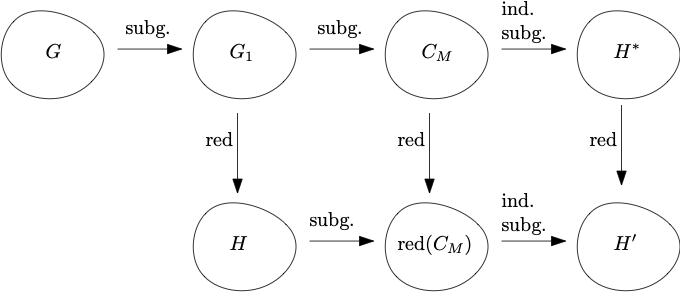
We also show that every large subgraph of an expander graph contains a large subgraph which is itself an expander.

A tournament $H$ is quasirandom-forcing if the following holds for every sequence $(G_n)_{n}$ of tournaments of growing orders: if the density of $H$ in $G_n$ converges to the expected density of $H$ in a random tournament, then $(G_n)_n$ is quasirandom. Every transitive tournament with at least 4 vertices is quasirandom-forcing (link), and Coregliano et al. showed that there is also a non-transitive 5-vertex tournament with the property (link). We show that no additional tournament has this property.

Random graph models with community structure have been studied extensively in the literature. For both the problems of detecting and recovering community structure, an interesting landscape of statistical and computational phase transitions has emerged. A natural unanswered question is: might it be possible to infer properties of the community structure (for instance, the number and sizes of communities) even in situations where actually finding those communities is believed to be computationally hard? We show the answer is no. In particular, we consider certain hypothesis testing problems between models with different community structures, and we show (in the low-degree polynomial framework) that testing between two options is as hard as finding the communities.

In addition, our methods give the first computational lower bounds for testing between two different `planted' distributions, whereas previous results have considered testing between a planted distribution and an i.i.d. `null' distribution.

Modularity is a quantity which has been introduced in the context of complex networks in order to quantify how close a network is to an ideal modular network in which the nodes form small interconnected communities that are joined together with relatively few edges. In this paper, we consider this quantity on a recent probabilistic model of complex networks introduced by Krioukov et al. (Phys. Rev. E 2010).

This model views a complex network as an expression of hidden hierarchies, encapsulated by an underlying hyperbolic space. For certain parameters, this model was proved to have typical features that are observed in complex networks such as power law degree distribution, bounded average degree, clustering coefficient that is asymptotically bounded away from zero, and ultra-small typical distances. In the present work, we investigate its modularity and we show that, in this regime, it converges to 1 in probability.

Temporal graphs, in which edges are active at specified times, are of relevance for spreading processes on graphs. In our setting the number of active times for each edge is fixed, but we can change the relative order in which (sets of) edges are active. We investigate the problem of determining an ordering of edges that minimises the maximum number of vertices reachable from any single starting vertex. Epidemiologically, this corresponds to the worst-case number of vertices infected in a single disease outbreak.

Determining the maximum modularity of a graph is known to be NP-complete in general, even to find a multiplicative approximation, but we show it has reduced complexity with respect to some structural parameterisations of the input graph.

On the other hand we prove modularity is W[1]-hard (and hence unlikely to admit an FPT algorithm) when parameterised simultaneously by pathwidth and the size of a minimum feedback vertex set.

Given a tree on $n$ vertices, we randomly label the vertices 1 to $n$. An occurence of a length $k$ permutation $\sigma$ is a sequence of vertices on a common descending path in the tree whose labels, when read from root to leaf, are ordered according to $\sigma$. We calculate the number of occurences of fixed length permutations in binary trees and split trees.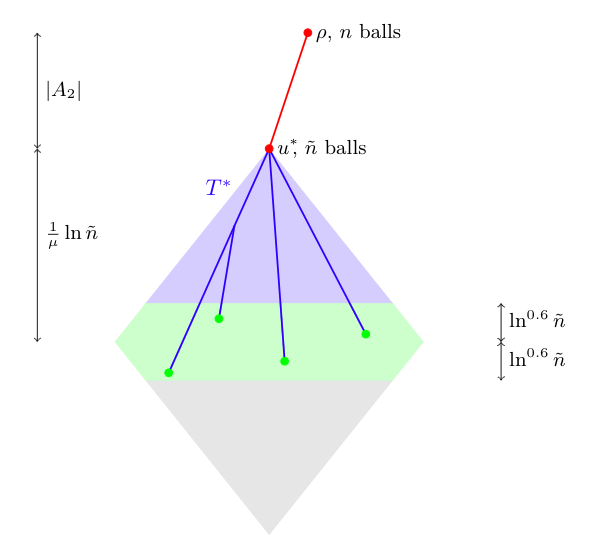
For the trees considered, this generalizes the inversion results below from $\sigma=21$ to more general permutations $\sigma$.
Conference version: Permutations in binary trees and split trees AofA

Modularity introduced by Newman and Girvan (in this paper) is a popular metric in community detection.
Two key features which we find for Erdos-Renyi random graphs are that the modularity is $1+o(1)$ with high probability (whp) for $np$ up to $1+o(1)$ (and no further); and when $np\geq 1$ and $p$ is bounded below 1, it has order $(np)^{-1/2}$ whp, in accord with a conjecture by Reichardt and Bornholdt in 2006 (and disproving another conjecture from the physics literature).
Conference version: AofA

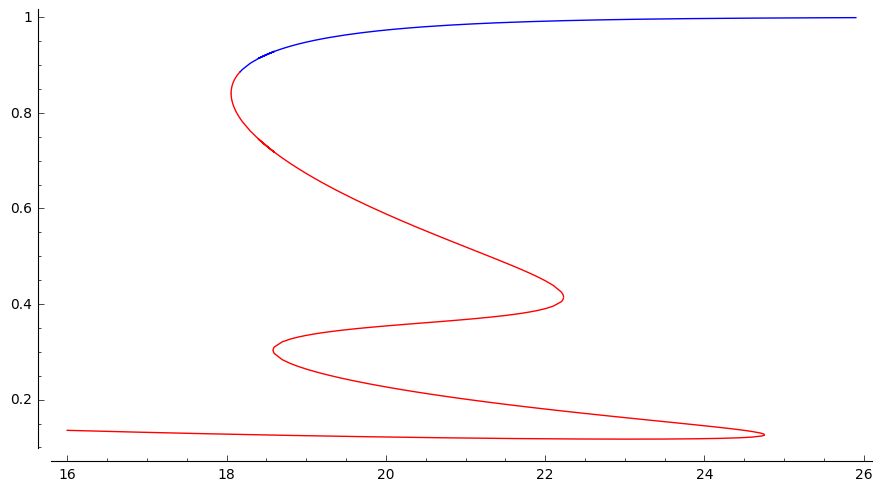We answer the following question of Joel Spencer:
Say that a set of trees $B$ follows the at-least-two rule if $t \in B$ if and only if the root of $t$ has two children $u$ and $v$ such that the subtrees rooted at $u$ and $v$ are also in $B$. Suppose that $\lambda > \lambda_{crit}$. Does there exist a set of trees $B$ with this metaproperty such that for random tree $T_\lambda$, we have that $\mathbb{P}[T_\lambda \in B]$ is the middle solution of the classical fixed point equation?

We define a new cutting process on trees the `blunt scissors' or $k$-cut model where each node must be cut $k$ times before it is destroyed. For $k=1$ this is the model of Meir and Moon. This paper studies the distribution of the $k$-cut number of a path on $n$ vertices.

We study $I(T)$, the number of inversions in a tree $T$ with its vertices labeled uniformly at random, which is a generalization of inversions in permutations. We first show that the cumulants of $I(T)$ have explicit formulas involving the $k$-total common ancestors of $T$ (an extension of the total path length). For three sequence of trees $T_n$ we consider $X_n$ the normalized version of $I(T_n)$.
We identify the limit of $X_n$ for complete $b$-ary trees. For $T_n$ being split trees, we show that $X_n$ converges to the unique solution of a distributional equation and when $T_n$’s are conditional Galton–Watson trees, we show that $X_n$ converges to a random variable defined in terms of Brownian excursions. By exploiting the connection between inversions and the total path length, we extend earlier results by Panholzer and Seitz. Conference version: [AofA]

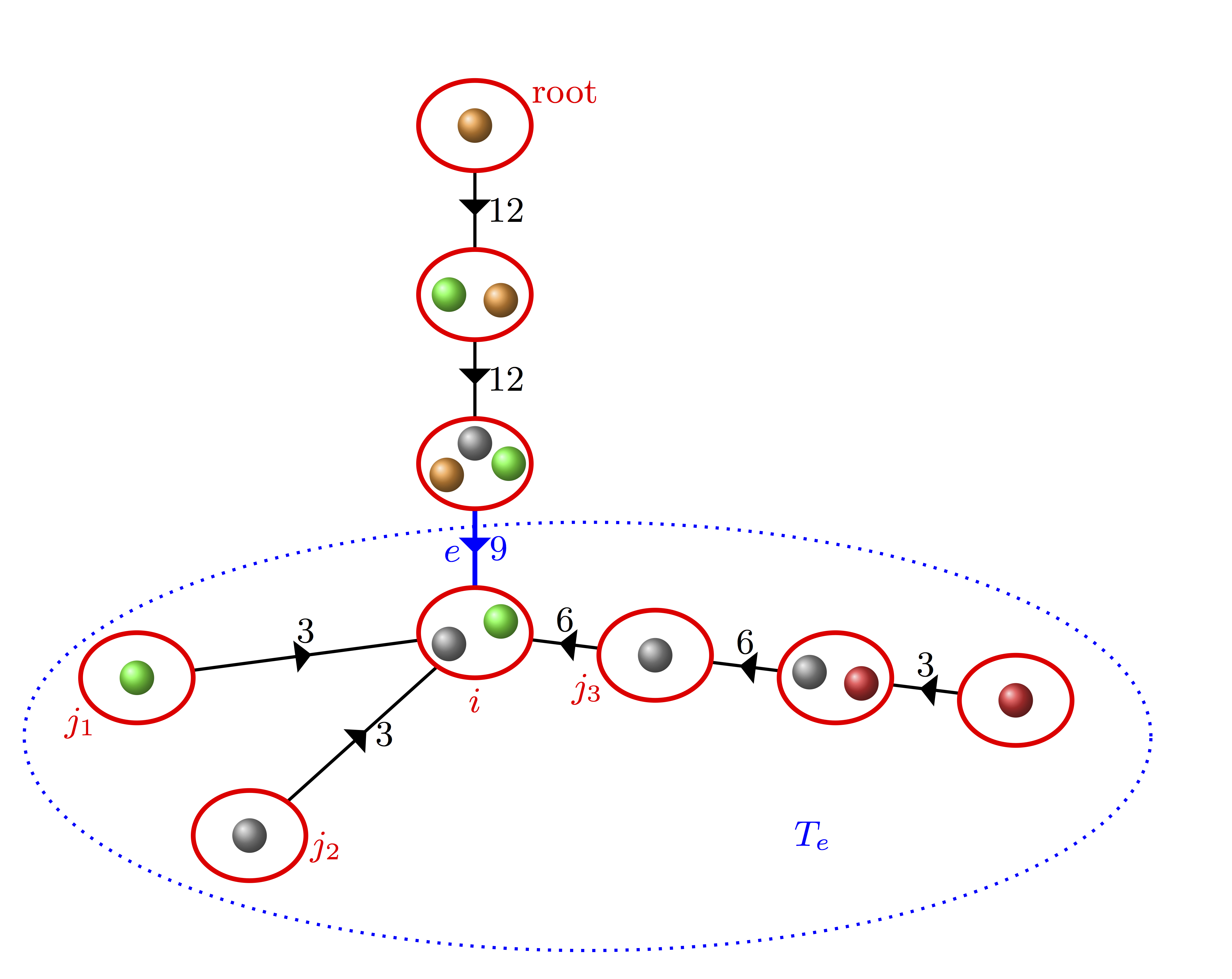Modularity introduced by Newman and Girvan (in this paper) is a popular metric in community detection.
We show that random cubic graphs usually have modularity in the interval (0.666, 0.804); and random $r$-regular graphs for large $r$ usually have modularity $\Theta(1/\sqrt{r})$. Our results give thresholds for the statistical significance of clustering found in large regular networks.
The modularity of cycles and low degree trees is known to be asymptotically 1. We extend these results to all graphs whose product of treewidth and maximum degree is much less than the number of edges. This shows for example that random planar graphs typically have modularity close to 1.

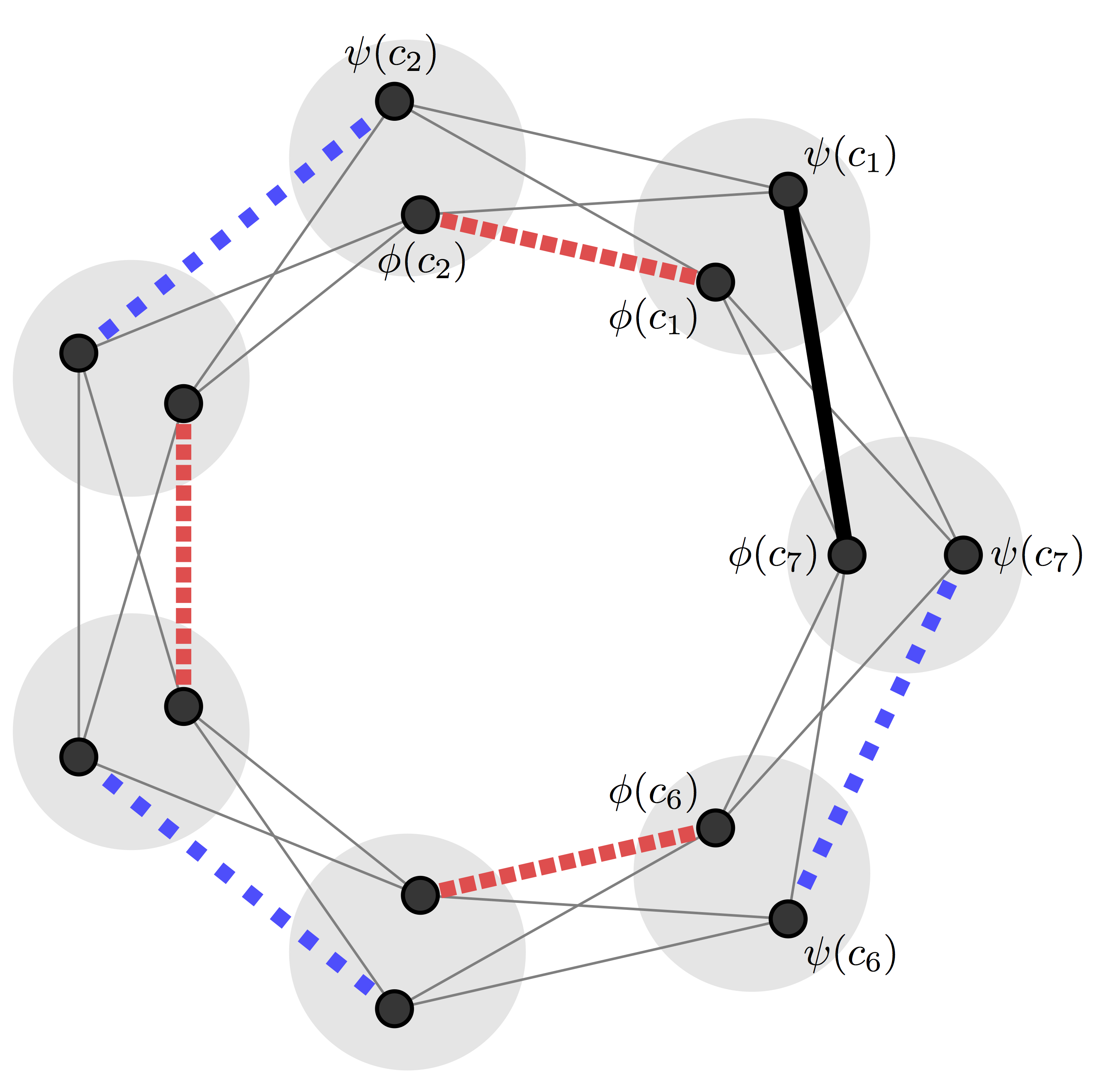For a given number of colours, $s$, the guessing number of a graph is the base $s$ logarithm of the size of the largest family of colourings of the vertex set of the graph such that the colour of each vertex can be determined from the colours of the vertices in its neighbourhood. We show that, for any given integer $s \geq 2$, if $a$ is the largest factor of $s$ less than or equal to $\sqrt{s}$, for sufficiently large odd $n$, the guessing number of the cycle $C_n$ with $s$ colours is $(n -1)/2 + \log_s (a)$. This answers a question posed in this paper by Christofides and Markstrom in 2011.

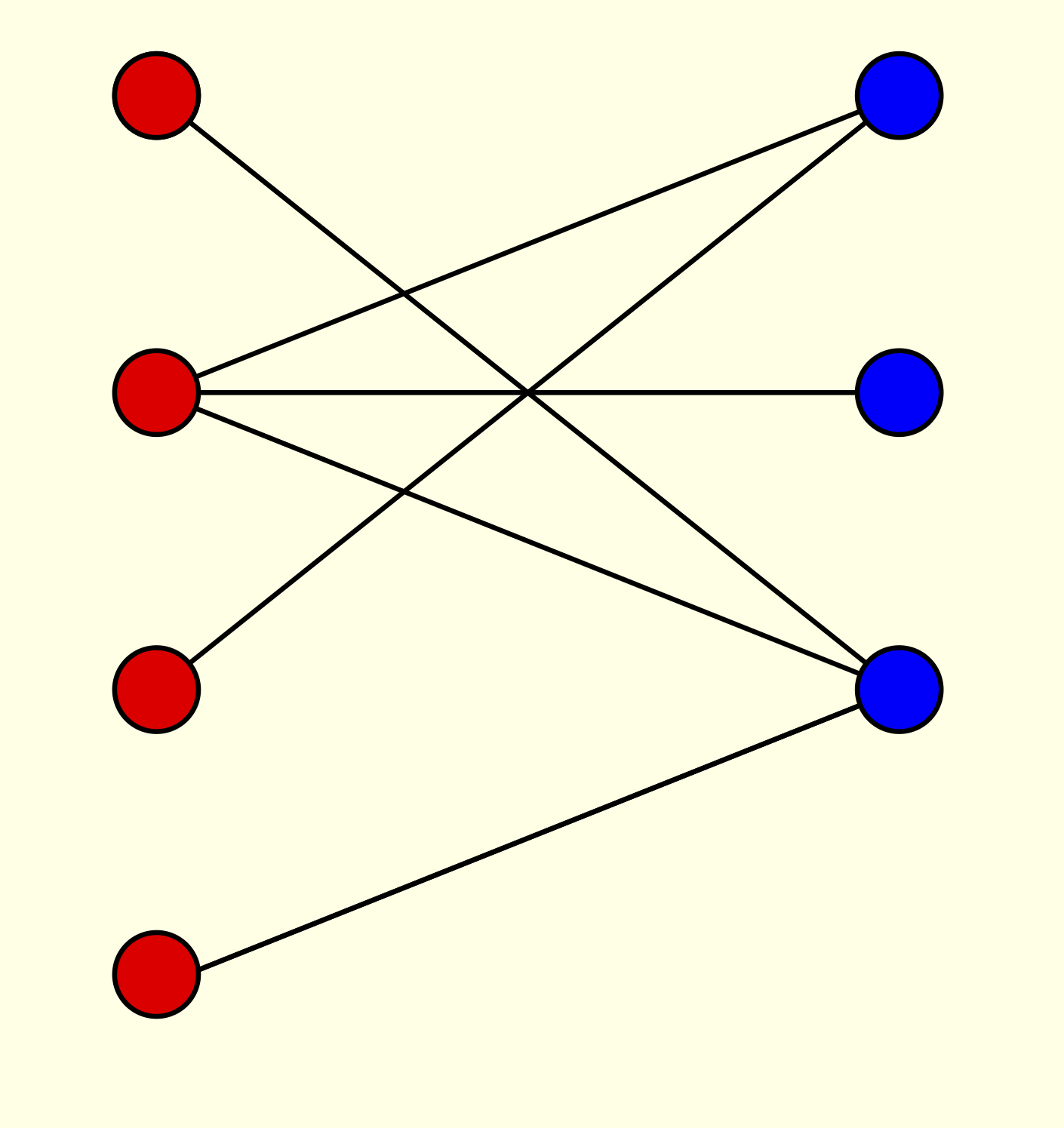We investigate the joint distribution of the vertex degrees in three models of random bipartite graphs. Namely, we can choose each edge with a specified probability, choose a specified number of edges, or specify the vertex degrees in one of the two colour classes.

In each case, provided the two colour classes are not too different in size nor the number of edges too low, we define a probability space based on independent binomial variables and show that its probability masses asymptotically equal those of the degrees in the graph model almost everywhere. The accuracy is sufficient to asymptotically determine the expectation of any joint function of the degrees whose maximum is at most polynomially greater than its expectation.

In this paper, we study $(1 : b)$ Avoider-Enforcer games played on the edge set of the complete graph on n vertices. For every constant $k \geq 3$ we analyse the $k$-star game, where Avoider tries to avoid claiming $k$ edges incident to the same vertex. We consider both versions of Avoider-Enforcer games - the strict and the monotone - and for each provide explicit winning strategies for both players. We determine the order of magnitude of the threshold biases $f_\mathcal{F}^{mon}$, $f_\mathcal{F}^{-}$ and $f_\mathcal{F}^{+}$, where $\mathcal{F}$ is the hypergraph of the game.